Talstelsels
Er zijn verschillende getalstelsels, en in de computerwereld wordt meestal met een speciaal getalstelsel
gewerkt.
Romeinse getallen zie je wel op oude gebouwen, waarop dan staat aangegeven wanneer het gebouwd is.
Daarbij worden de letters I, V, X, enz. gebruikt. Die letters hebben een bepaalde waarde:
I = 1
V = 5
X = 10
L = 50
C = 100
D = 500
M = 1000
Als er meerdere letters gebruikt worden moet je die gewoon bij elkaar optellen.
Behalve als er een letter met een grotere waarde achter staat, dan moet je de waarde er van aftrekken.
Dus:
II = 2
III = 3
IV = 4
VI = 6
VII = 7
VIII = 8
IX = 9
XX = 20
XXX = 30
XL = 40
MMCMLXVI = 2966
Een nadeel van deze notatie is dat je erg lange en onoverzichtelijke getallen krijgt.
In ons
decimale of tientallige getalstelsel gebruiken we maar 10 symbolen (cijfers) namelijk 0, 1, 2, 3, 4, 5, 6, 7, 8 en 9.
De waarde die de cijfers hebben hangt af van hun plaats, bijvoorbeeld:
3847 = 7 + 40 + 800 + 3000 = 7 + 4 x 101 + 8 x 102 + 3 x 103
In de computerwereld wordt meestal gewerkt met het
binaire of
tweetallige getalstelsel.
Daarin worden maar twee tekens gebruikt, namelijk 0 en 1.
Omdat een bit maar twee waarden kan aannemen, namelijk 0 en 1, is het tweetallig getalstelsel het voor de hand
liggende systeem voor de computer.
In het tientallig stelsel moet je een getal van achter naar voren lezen. Het laatste cijfer blijft gelijk, het cijfer daarvoor moet
keer 10, het cijfer daarvoor moet keer 100 (=10
2), het cijfer daarvoor moet keer 1000 (=10
3), enz.
In het binaire getalstelsel moet je een getal ook van achter naar voren lezen.
Het laatste cijfer blijft weer gelijk, het cijfer daarvoor moet
keer 2, het cijfer daarvoor moet keer 4 (=22), het cijfer daarvoor moet keer 8 (=23),
enz.
De decimale waarde van een binair getal kun je dus op de volgende manier bepalen:
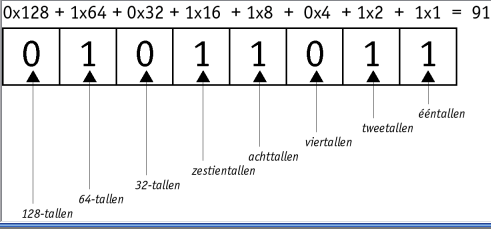
101 = (van achter naar voor) 1 + 0 x 2 + 1 x 4 = 5
11011010 = 0 + 1 x 2 + 0 x 4 + 1 x 8 + 1 x 16 + 0 x 32 + 1 x 64 + 1 x 128 = 2 + 8 + 16 + 64 + 128 = 218
11111111 = 1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 = 255,
en dat is het grootste getal dat met een byte is te maken!
Hoe maak je van een decimaal getal een binair getal?
Je kijkt eerst wat de grootste macht van 2 is die kleiner of gelijk aan je getal is.
Die macht van 2 trek je van je getal af, en dan ga je op dezelfde manier verder met de rest.
Neem bv 29
16 is een macht van 2 (16 = 24) en kleiner dan 29, de volgende macht (32 = 25)) is te groot.
29 - 16 = 13. De grootste macht van 2 kleiner of gelijk 13 is 8 (8 = 23).
13 - 8 = 5. de grootste macht van 2 kleiner of gelijk 5 is 4 (4 = 22)
5 - 4 = 1
dus 29 = 16 + 8 + 4 + 1 = 24 + 23 + 22 + 20
binair is dat dus 11101
Voer zelf de voorbeelden in... klik hier
Een andere manier werkt als volgt:
Deel het getal steeds door 2 (totdat de uitkomst 0 is) en schrijf de rest op (die kan dus 0 of 1 zijn)
Schrijf daarna de resten achter elkaar (achterstevoren) op, en je hebt de uitkomst.
Voorbeeld (we nemen weer 29)
29 delen door 2 is 14, rest 1
14 delen door 2 is 7, rest 0
7 delen door 2 is 3, rest 1
3 delen door 2 is 1, rest 1
1 delen door 2 is 0, rest 1
De resten in omgekeerde volgorde geven het binaire getal: 11101
Nog een voorbeeld: 205
205 is kleiner dan 256, dus het is in één byte (dus 8 bits) te schrijven.
De machten van twee die daarin voorkomen zijn 128, 64, 32, 16, 8, 4, 2 en 1
205: zit 128 er in? Ja, schrijf een 1 op.
205 - 128 = 77
77: zit 64 er in? Ja, schrijf een 1 op.
77 - 64 = 13
13: zit 32 er in? Nee, schrijf een 0 op.
13: zit 16 er in? Nee, schrijf een 0 op.
13: zit 8 er in? Ja, schrijf een 1 op.
13 - 8 = 5
5: zit 4 er in? Ja, schrijf een 1 op.
5 - 4 = 1
1: zit 2 er in? Nee, schrijf een 0 op.
1: zit 1 er in? Ja, schrijf een 1 op.
1 - 1 = 0, klaar
Dus 205 (decimaal) = 11001101 (binair)
Naast het binaire en het decimale getalstelsel wordt in de informatica ook nog het
hexadecimale of
zestientallige getalstelsel gebruikt.
In het zestientallige of hexadecimale getalstelsel worden zestien tekens (cijfers genoemd) gebruikt.
Naast de cijfers 0 t/m 9 worden
ook de hoofdletters A t/m F gebuikt, met als waarden 10 t/m 15.
| decimaal |
hexadecimaal |
binair |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 2 | 10 |
| 3 | 3 | 11 |
| 4 | 4 | 100 |
| 5 | 5 | 101 |
| 6 | 6 | 110 |
| 7 | 7 | 111 |
| 8 | 8 | 1000 |
| 9 | 9 | 1001 |
| 10 | A | 1010 |
| 11 | B | 1011 |
| 12 | C | 1100 |
| 13 | D | 1101 |
| 14 | E | 1110 |
| 15 | F | 1111 |
| 16 | 10 | 1 0000 |
| 17 | 11 | 1 0001 |
| 18 | 12 | 1 0010 |
| 19 | 13 | 1 0011 |
| 20 | 14 | 1 0100 |
In het hexadecimale getalstelsel lees je een getal, net zo als bij een binair en decimaal getal,
ook van achter naar voren.
Het laatste
cijfer blijft weer gelijk, het cijfer daarvoor moet
keer 16, het cijfer daarvoor moet keer 256 (=162), enz.
In de informatica worden eigenlijk alleen maar hexadecimale getallen van twee cijfers gebruikt.
Voorbeelden:
35 (hexadecimaal) = 3 x 16 + 5 = 53 (decimaal)
4B (hexadecimaal) = 4 x 16 + 11 = 75 (decimaal)
A7 (hexadecimaal) = 10 x 16 + 7 = 167 (decimaal)
BD (hexadecimaal) = 11 x 16 + 13 = 189 (decimaal)
FF (hexadecimaal) = 15 x 16 + 15 = 255 (decimaal), dus het grootste hexadecimale getal van twee cijfers is 255.
En dat is ook het
grootste binaire getal van 8 bits, dus een byte.
Dat is ook de reden dat hexadecimale getallen veel gebruikt worden in de informatica: getallen die in een byte passen zijn met twee
tekens te schijven in het hexadecimale getalstelsel.
Hoe maak je van een decimaal getal (kleiner dan 256) een hexadecimaal getal?
-
Deel het getal door 16
- Schrijf het getal dat er uitkomt op, en de rest er achter.
- Maar denk er om dat als de uitkomst of de rest groter dan 9 is, je 10 moet vervangen door A, 11 door B, 12 door C, 13 door D, 14 door E en 15 door F.
Neem bv 199
199 gedeeld door 16 is 12, en de rest is 7
Vervang 12 door C, dan is het antwoord dus C7
Hexadecimale getallen kom je bijvoorbeeld tegen in HTML-documenten, bij het aangeven van kleuren.
Met
bgcolor="#FF0098" geef je aan wat de achtergrondkleur van de webpagina is.
Je moet dan FF0098 verdelen in drie groepjes van 2: FF geeft aan wat de hoeveelheid rood is, maar dan als hexadecimaal getal,
00 geeft aan geeft aan wat de hoeveelheid geel is en 98 geeft de hoeveelheid blauw als hexadecimaal getal.
