Logische poorten (2)

In een computer is een bit eigenlijk een schakeling, die open en dicht kan staan.
Zo'n schakelaar heet ook wel een transistor. Er zitten miljoenen transistoren op een chip van een vierkante centimeter.
Schakelaars kunnen met elkaar verbonden worden door middel van een schakeling, en zo'n schakeling kan er voor zorgen dat een andere schakelaar in een bepaalde stand komt te staan.
Je kunt daarbij denken aan lichtschakelaars, die aan of uit kunnen staan, en die zijn dus te vergelijken met een bit.
Je kunt ook denken aan een lamp, die aan of uit kan staan, en die dus ook te vergelijken is met een bit.

Je hebt verschillende soorten schakelingen.
Bekijk de schakeling hieronder maar eens, dat is de zogenaamde en-schakeling.



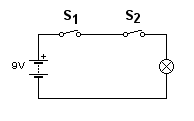
S1 en S2 zijn schakelaars, en het rondje met het kruisje er in stelt een lamp voor. Verder zie je een voeding.
Bij deze schakeling brandt de lamp alleen als schakelaar 1 en schakelaar 2 beide gesloten zijn, dus aan staan.
Daarom wordt dit wel een en-schakeling genoemd, of in het engels een AND-poort.
We kunnen de mogelijke standen van de schakelaars S1 en S2 met de gevolgen voor de lamp in een tabel weergeven:

S1	S2		X (lamp)
0	0		0
0	1		0
1	0		0
1	1		1

Behalve de AND-poort is er ook een OR-poort (Nederlands: OF-schakeling).
Die ziet er als volgt uit:



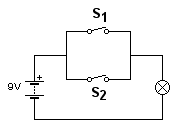
S1 en S2 zijn weer schakelaars, en het rondje met het kruisje er in is weer een lamp.
Bij deze schakeling brandt de lamp als schakelaar 1 of schakelaar 2 gesloten is (of allebei).
De tabel die hierbij hoort ziet er als volgt uit:

S1	S2		X (lamp)
0	0		0
0	1		1
1	0		1
1	1		1

Tenslotte is er nog de XOR-poort (Nederlands: XOF-schakeling).
Die ziet er als volgt uit:



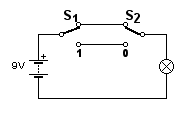
S1 en S2 zijn weer schakelaars. S1 staat aan als de schakelaar naar beneden staat (daarom staat bij de onderkant een 1) en S2 staat aan als de schakelaar naar boven staat (daarom staat bij de onderkant een 0).
Bij deze schakeling brandt de lamp als schakelaar 1 of schakelaar 2 aan is, maar niet allebei; daarom wordt wel het exclusieve of genoemd, en daarom staat er een X voor het woordje of (de x van exclusief).
Dit wordt ook wel een hotel-schakeling genoemd. Vrijwel elk huis met een trap heeft zo'n schakeling voor het traplicht. Het licht kan bediend worden met twee schakelaars, één voor onder en één voor boven.
De tabel die hierbij hoort ziet er als volgt uit:

S1	S2		X (lamp)
0	0		0
0	1		1
1	0		1
1	1		0

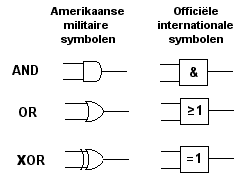
Er zijn speciale symbolen voor de logische poorten ontworpen door de Amerikaanse defensie. Later zijn er ook internationale afspraken gemaakt voor dit soort symbolen, maar de Amerikaanse militaire symbolen worden toch nog heel vaak gebruikt. Je ziet ze hier onder.



Met behulp van logische schakelingen kun je eenvoudige optellingen van bits maken. Kijk eerst naar het optellen van twee 1-bits getallen.



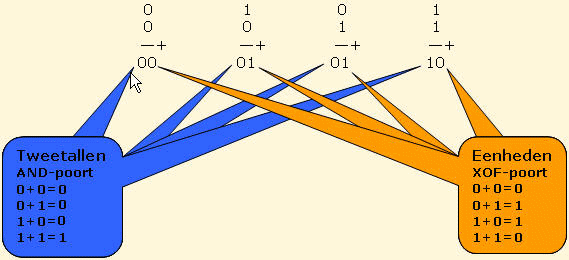
Wanneer je de uitkomst van bovenstaande sommetjes vergelijkt met de tabellen van de verschillende poorten, dan blijkt dat de eenheden (het achterste bit van de uitkomst) bepaald worden door een XOF-poort en de tweetallen (het voorste bit van de uitkomst) door een AND-poort.
Met behulp van een AND- en XOF-poort kun je dus een 'Een-Bit-Opteller' bouwen. Deze schakeling wordt ook wel een 'Half Adder' genoemd, zie hier onder.



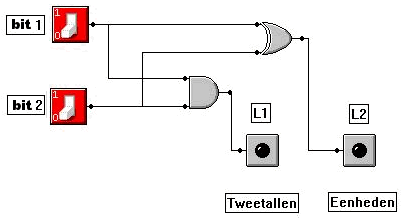
Een 'Half Adder'-schakeling is dus een belangrijke elektronische component die gebruikt wordt bij het optellen van bits. De schakelingen worden een stuk ingewikkelder als er grotere getallen moeten worden opgeteld.
In paragraaf 1.3 is uitgelegd hoe je zelf grotere binaire getallen kunt optellen: je begint dan met de achterste bits en dan werk je naar voren, en je moet steeds kijken wat je moet onthouden.

Als je een schakeling wilt maken voor de optelling van grotere getallen, bijvoorbeeld van twee bytes, dan moet de computer het op dezelfde manier doen, dus ook steeds iets onthouden.

De schakeling die je nodig hebt om dit probleem op te lossen is de 'Full Adder'-schakeling. Deze schakeling zorgt er voor dat er drie bits worden opgeteld: de twee bits van de twee getallen en de carry-in.

Een 'Full Adder'-schakeling ziet er als volgt uit:



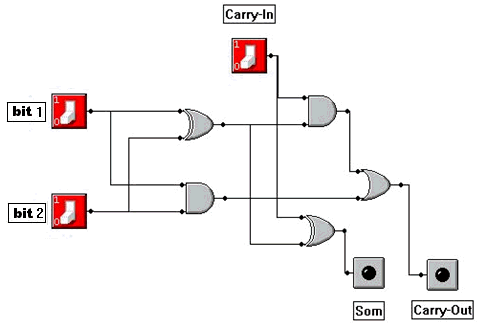Carry-in is het onthouden van de vorige optelling en carry-out is het onthouden voor de volgende optelling.

Een 'Full Adder'-schakeling is dus een schakeling die als onderdeel gebruikt wordt bij een schakeling voor het optellen van binaire getallen die bestaan uit meer dan 1 bit.
Hier onder zie je dan de schakeling voor het optellen van twee getallen die beide uit 2 bits bestaan : de 'Twee Bits Teller'.