Het tweetallig (binair) stelsel
In plaats van de tien tekens van het tientallige stelsel, gebruiken we er nu maar twee: 0 en 1
In plaats van de tien tekens van het tientallige stelsel, gebruiken we er nu zestien: 0 tm 9 aangevuld met zes letters A tm F
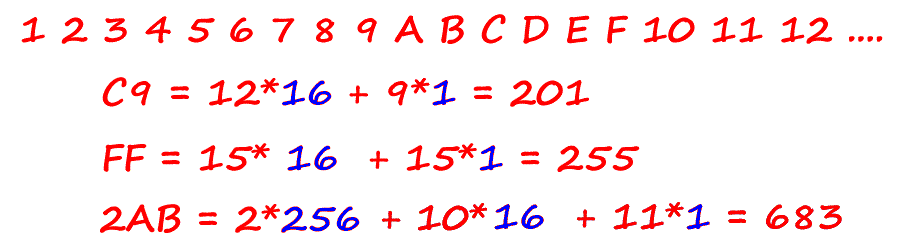
In ons decimaal stelsel groeperen we lange getallen vaak in groepjes van drie cijfers.
En soms zetten we daar zelfs puntjes tussen. Vergelijk maar eens 189542392 en 189.542.392 (honderdnegentachtig miljoen vijfhonderttweeënveertiggduizend driehonderdtweeënnegentig).
Hoe meer symbolen je hebt, hoe korter de boodschap kan zijn. Denk maar aan een chinees karakter dat een compleet
menu kan uitbeelden. Omgekeerd geldt: als je maar twee tekens hebt, -een nul en een èèn-, dan heb je wel veel tekens nodig.
Een voorbeeld hiervan is het €-teken (Unicode +20AC).
Dit teken wordt in de computer voorgesteld door 0010 0000 1010 1100.
Om zo'n lange reeks (16, twee bytes) korter weer te geven is het 16 tallig stelsel bedacht.
De byte(s) worden daartoe verdeeld in groepjes van vier *), en elk groepje wordt aangeduid met de decimale waarde. Deze decimale waarde is minimaal 0 en maximaal 15.
We hebben dan wat extra symbolen nodig voor 10 (A), 11 (B), 12 (C), 13 (D), 14 (E) en 15 (F).
*) Dit lijkt een beetje op onze gewoonte om in het decimale stelsel de cijfers te groeperen in groepjes van drie,
zodat je snel kunt zien om welk getal het gaat.